惯性矩的定义与计算方法

惯性矩，作为描述截面抵抗弯曲性质的重要物理量，广泛应用于结构设计和工程计算中。为了更好地理解这一概念，本文将详细探讨惯性矩的公式以及如何进行计算。

惯性矩的公式是什么？

惯性矩（Moment of Inertia），也称为质量惯性矩，是衡量物体对旋转方向变化阻力的一个物理量。惯性矩的大小取决于物体中质量相对于旋转轴的分布情况。对于点质量，惯性矩是质量乘以与旋转参考轴垂直距离的平方，其公式为：

\[I = m r^2\]

其中：

\(I\) 表示惯性矩（单位：\(kg \cdot m^2\)，\(slug \cdot ft^2\)，\(lbf \cdot fts^2\)）

\(m\) 表示质量（单位：\(kg\)，\(slugs\)）

\(r\) 表示轴与旋转质量之间的距离（单位：\(m\)，\(ft\)）

然而，在实际应用中，我们面对更多的是复杂形状和分布的物体，这时需要采用积分或特定形状的惯性矩公式来计算。

矩形截面的惯性矩

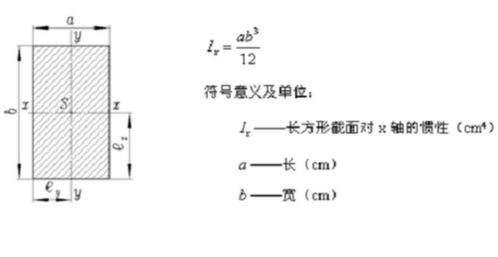
矩形截面的惯性矩常用于梁和板等结构元件的设计。对于矩形截面，如果旋转轴位于其中心，则惯性矩公式为：

\[I = \frac{b \cdot h^3}{12}\]

其中：

\(b\) 表示矩形的宽度

\(h\) 表示矩形的高度

如果旋转轴沿着矩形截面的边缘，例如沿宽度方向，则惯性矩为：

\[I = \frac{1}{3} \cdot m \cdot a^2\]

其中：

\(m\) 表示矩形的质量

\(a\) 表示边缘到旋转轴的距离（即矩形的高度或宽度，视旋转轴的位置而定）

三角形截面的惯性矩

三角形截面的惯性矩在设计和计算桁架、框架等结构时也十分关键。对于等腰三角形截面，如果旋转轴位于其底边的中心且垂直于底边，则惯性矩公式为：

\[I = \frac{b \cdot h^3}{36}\]

其中：

\(b\) 表示三角形的底边长度

\(h\) 表示三角形的高度

圆形截面的惯性矩

圆形截面是工程设计中常见的形状之一，其惯性矩对于计算轴的弯曲、轴的扭转等问题具有重要意义。对于实心圆形截面，如果旋转轴位于圆心且垂直于截面，则惯性矩公式为：

\[I = \frac{\pi \cdot d^4}{64}\]

其中：

\(d\) 表示圆的直径

或者，如果使用半径 \(r\)，则公式为：

\[I = \frac{\pi \cdot r^4}{4}\]

环形截面的惯性矩

环形截面，即空心圆形截面，也常用于轴、管等结构的设计。对于环形截面，其惯性矩公式为：

\[I = \frac{\pi \cdot D^4 \cdot (1 - \alpha^4)}{64}\]

其中：

\(D\) 表示环形的外直径

\(\alpha\) 表示环形截面的内外直径比，即 \(\alpha = \frac{d}{D}\)，其中 \(d\) 为内直径

惯性矩的计算方法

在实际计算中，通常需要先确定物体的截面形状和尺寸，然后根据相应的公式计算惯性矩。以下是一个计算惯性矩的示例：

示例：计算矩形梁的惯性矩

假设有一矩形梁，宽度 \(b = 0.3m\)，高度 \(h = 0.6m\)，且旋转轴位于其截面中心。

1. 根据矩形截面惯性矩公式：

\[I = \frac{b \cdot h^3}{12}\]

2. 代入 \(b\) 和 \(h\) 的值：

\[I = \frac{0.3 \cdot 0.6^3}{12} = \frac{0.3 \cdot 0.216}{12} = 0.0054 \text{ } m^4\]

因此，该矩形梁的惯性矩为 \(0.0054 \text{ } m^4\)。

示例：计算圆形轴的惯性矩

假设有一实心圆形轴，直径 \(d = 0.1m\)。

1. 根据圆形截面惯性矩公式：

\[I = \frac{\pi \cdot d^4}{64}\]

2. 代入 \(d\) 的值：

\[I = \frac{\pi \cdot 0.1^4}{64} = \frac{\pi \cdot 0.0001}{64} \approx 0.00000493 \text{ } m^4\]

因此，该圆形轴的惯性矩约为 \(0.00000493 \text{ } m^4\)。

注意事项

1. 截面选择：在计算惯性矩时，需要选择正确的截面形状和尺寸，并确定旋转轴的位置。

2. 单位统一：确保计算过程中所有物理量的单位一致，以避免计算错误。

3. 近似计算：对于复杂形状或不规则截面的物体，可能需要采用近似计算方法或借助计算机辅助设计（CAD）软件进行计算。

4. 结构分析：在计算惯性矩时，还需要考虑物体的材料、边界条件等因素，以确保结构设计和计算的准确性。

结语

惯性矩作为衡量物体对旋转方向变化阻力的物理量，在结构设计和工程计算中具有重要作用。本文介绍了矩形、三角形、圆形和环形等常见截面形状的惯性矩公式及其计算方法，并通过示例进行了详细说明。希望读者能够掌握这些基础知识，并在实际应用中灵活运用。同时，也需要注意截面选择、单位统一、近似计算和结构分析等方面的问题，以确保结构设计和计算的准确性和可靠性。