鸽巢原理

在数学的广阔天地里，隐藏着无数令人着迷的原理与定理，它们如同璀璨星辰，指引着人类探索未知世界的航程。其中，“抽屉原理”，这一看似简单却蕴含深刻哲理的数学思想，不仅在数学领域内大放异彩，更在日常生活、计算机科学、密码学乃至哲学思考中找到了其独特的用武之地。本文将从多个维度出发，带您一窥“抽屉原理”的奥秘与魅力。

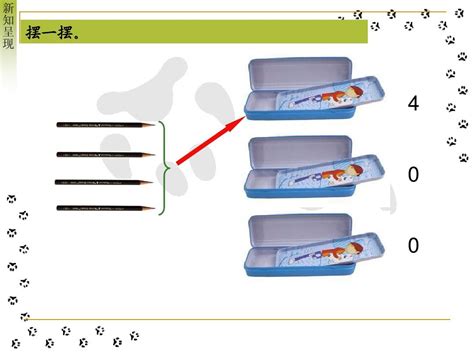
一、原理初探：数学的奇妙巧合

“抽屉原理”，又称“鸽巢原理”，是一种组合数学的经典定理。其核心思想可以简述为：如果将多于n个物体放入n个容器中，则至少有一个容器内含有两个或两个以上的物体。这个原理初听起来似乎平凡无奇，但正是这份朴素之中蕴含着解决问题的强大力量。想象一下，如果你有5双袜子（10只）需要放入4个抽屉中，无论你怎么分配，总会有至少一个抽屉里放着不止一只袜子——这便是抽屉原理的直接体现。

二、生活应用：从聚会到职业规划

抽屉原理不仅限于数学书本上的抽象概念，它在现实生活中的应用同样广泛而深刻。以一次家庭聚会为例，假设有11位客人（假设不考虑性别、年龄等因素，仅作为数字示例），而房间里只有10把椅子可供就坐。根据抽屉原理，至少会有两把椅子上坐着不止一位客人，即至少有一对客人需要共享座位，或者有人得站着。虽然这在实际操作中可能不太现实，但它形象地说明了当资源有限而需求超出时，资源分配的不均衡是必然的。

在职业规划领域，抽屉原理也提醒我们，面对有限的职位和发展空间，激烈的竞争在所难免。正如众多求职者竞争少量高薪岗位，只有不断提升自我，才能在众多“物体”中脱颖而出，避免成为那个“被挤占的抽屉”。

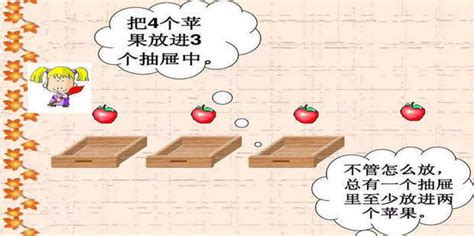
三、计算机科学：算法设计与优化

计算机科学是抽屉原理大显身手的另一片沃土。在算法设计中，抽屉原理常被用于证明某些算法的正确性或效率。例如，在解决“找出n个数中的第二大的数”的问题时，可以利用抽屉原理简化算法复杂度。我们不需要对所有数进行排序，而是维护两个变量分别记录当前遇到的最大数和次大数，遍历一遍数组即可完成任务。这里，虽然不直接用到“抽屉”和“物体”的比喻，但背后的逻辑——在有限的空间（两个变量）内处理无限可能的数据（n个数），正是抽屉原理的精髓所在。

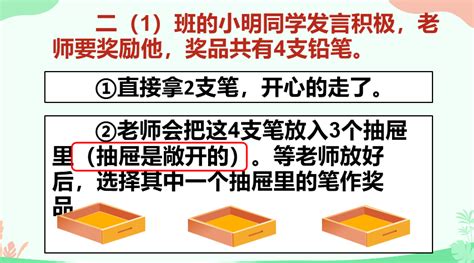
此外，在哈希函数的设计、数据库索引优化等方面，抽屉原理也提供了重要的理论支撑。它告诉我们，当数据量超过存储结构的容量时，冲突（即多个元素映射到同一位置）是不可避免的，关键在于如何有效地处理和解决这些冲突，以提高系统的整体性能。

四、密码学：安全与攻击的博弈

密码学是另一个受益于抽屉原理的领域。在密码分析中，攻击者往往试图通过有限的信息（如密文）推断出密钥或明文内容。抽屉原理在这里表现为，如果密钥空间足够大，而攻击者能尝试的密钥数量有限，那么存在某个密钥（或明文）使得攻击者找到它的概率极低，从而保证了密码系统的安全性。换句话说，密码学中的“锁”（密钥空间）相对于“钥匙”（攻击者能尝试的密钥）足够多，使得“一把钥匙开一把锁”的规则在大多数情况下不成立，从而达到了保护信息安全的目的。

五、哲学思考：存在与选择的悖论

跳出具体应用的范畴，抽屉原理还引发了深刻的哲学思考。它揭示了宇宙万物在有限与无限、确定与随机之间的微妙平衡。从某种角度看，每个人的生命经历、思想观念都可以视为“物体”，而社会、环境则是容纳这些“物体”的“抽屉”。在有限的时间和空间里，我们如何做出选择，如何在众多可能性中找到自己的位置，成为了每个人必须面对的问题。

抽屉原理提示我们，无论是个人的成长还是社会的进步，都不可避免地会遇到资源有限与需求无限的矛盾。这要求我们在面对选择时，既要勇于探索未知，又要学会在有限条件下做出最优决策，同时也要接受并适应生活中的不确定性和多样性。

六、结语：从数学到生活的桥梁

综上所述，抽屉原理作为一种基础的数学原理，其影响力远远超出了数学学科的范畴，成为连接数学与生活、理论与实践、确定与随机的桥梁。它教会我们如何在有限中寻找可能，在冲突中寻求平衡，在不确定中做出决策。无论是解决日常生活中的小问题，还是探索宇宙的奥秘，抽屉原理都是一把开启智慧之门的钥匙，引领我们不断前行，在知识的海洋中遨游，在生活的舞台上绽放光彩。

正如数学中的许多原理一样，抽屉原理的价值不仅仅在于其本身的正确性，更在于它激发了我们对于世界的好奇心和探索欲，促使我们不断思考、学习和创新。在这个过程中，我们不仅加深了对数学的理解，也收获了关于生活、关于自我的深刻洞见。