等边三角形面积的计算公式是什么？

等边三角形的面积公式探秘

在数学的世界里，几何图形以其独特的魅力和广泛的应用性，一直吸引着无数人的探索与发现。而在这丰富多彩的几何图形中，等边三角形以其简洁、匀称的外观和独特的性质，成为了众多学者和爱好者研究的焦点。今天，我们就来一起揭开等边三角形面积公式的神秘面纱，看看这个简单而又美妙的公式背后隐藏的数学奥秘。

等边三角形，顾名思义，就是三边长度相等的三角形。它的三个内角也都是相等的，每个角都是60度。这种独特的性质使得等边三角形在几何学中占有举足轻重的地位。无论是在建筑、艺术还是科学研究中，等边三角形都以其独特的美感和实用性而受到人们的青睐。

那么，如何计算等边三角形的面积呢？这或许是许多人在初次接触等边三角形时都会产生的疑问。事实上，计算等边三角形的面积并不复杂，只需要掌握一个简单的公式即可。

我们先来回顾一下三角形面积的一般公式。对于任意一个三角形，其面积都可以通过以下公式来计算：

面积 = (底 × 高) ÷ 2

在这个公式中，“底”和“高”是三角形的两个关键要素。底是三角形任意一边的长度，而高则是从这条边出发，垂直于这条边并到达三角形另一顶点的线段。

然而，对于等边三角形来说，由于其三边长度相等，我们可以选择任意一边作为底。同时，由于等边三角形的三个内角都是60度，其高也具有一种特殊的性质：它不仅是垂直于底的线段，还是将等边三角形分为两个全等的30-60-90直角三角形的关键线段。

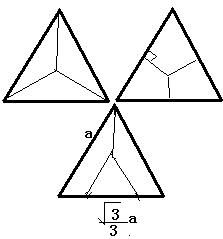
在这种特殊情况下，我们可以利用等边三角形的边长来直接计算其高。设等边三角形的边长为a，那么其高h可以通过以下公式来计算：

h = a × √3 ÷ 2

这里的√3表示根号下的3，是一个无理数。通过这个公式，我们可以很方便地求出等边三角形的高。

现在，我们已经知道了等边三角形的底和高，就可以利用三角形面积的一般公式来计算其面积了。将底a和高h代入公式，我们得到：

面积 = (a × (a × √3 ÷ 2)) ÷ 2

= (a^2 × √3) ÷ 4

这就是等边三角形面积的计算公式。通过这个公式，我们可以很方便地求出任意一个等边三角形的面积，只需要知道其边长a即可。

当然，除了这个公式之外，等边三角形的面积还可以通过其他方法来计算。例如，我们可以利用向量的点积公式或者三角形的外接圆和内切圆等性质来推导其面积公式。但是，这些方法相对来说比较复杂，不如直接利用等边三角形的边长来计算面积来得直接和简便。

值得一提的是，等边三角形的面积公式在数学和物理学等领域都有着广泛的应用。在建筑设计中，设计师们常常利用等边三角形的面积公式来计算各种几何形状的面积和体积，从而确保建筑物的稳定性和美观性。在物理学中，等边三角形的面积公式也被广泛应用于计算电场、磁场等物理场的分布和强度。

此外，等边三角形的面积公式还与许多其他数学定理和公式有着密切的联系。例如，它与勾股定理、三角函数、圆的性质等都有着千丝万缕的联系。通过学习和掌握这些定理和公式，我们可以更加深入地理解等边三角形的面积公式，从而在数学和物理学等领域中更加自如地运用它。

在探索等边三角形面积公式的过程中，我们不禁会感叹数学的奇妙和魅力。这个看似简单的公式背后，隐藏着许多深刻的数学原理和奥秘。通过学习和掌握这个公式，我们不仅可以提高自己的数学素养和思维能力，还可以更加深入地理解自然界的奥秘和规律。

当然，数学的学习并不是一蹴而就的。在掌握等边三角形面积公式的过程中，我们可能会遇到各种困难和挑战。但是，只要我们保持好奇心和求知欲，勇于探索和实践，就一定能够克服这些困难，掌握更多的数学知识和技能。

最后，让我们再次回顾一下等边三角形的面积公式：面积 = (a^2 × √3) ÷ 4。这个公式虽然简单，但是它却蕴含着丰富的数学思想和应用价值。希望每一位读者都能够通过这个公式，感受到数学的魅力所在，并在学习和探索的道路上不断前行。

在未来的学习和生活中，愿我们都能够保持一颗好奇和求知的心，勇于探索未知的世界，不断追求真理和智慧的光芒。让我们一起在数学的海洋中遨游吧！